Binary Search Algorithm

1 bit - 1, 0 1 byte - 8 bits, 256 values

🔄 Decimal to Binary (Divide by 2 Method) Steps:

Divide the number by 2
Record the remainder
Repeat until the quotient is 0
Read the remainders bottom to top

📘 What is Binary Search? Binary Search is a powerful algorithm used to quickly find an element in a sorted list by repeatedly dividing the search interval in half. Binary search is much faster than linear search for large datasets. It’s often referred to as a “divide and conquer” algorithm.

Steps:

Check the middle element
If it’s the target, return it
If not, search the left or right half
Repeat until found or empty

⏱️ Time Complexity of Binary Search

Binary search is efficient because it divides the search space in half with every step. Here’s how its time complexity breaks down:
🧠 At each step, we eliminate half of the remaining elements.
🧮 This “halving” continues until there’s only one element left.
✨ This gives us a logarithmic number of steps — specifically: Time Complexity: O(log₂ n) Where n is the number of elements in the list.

Why O(log n)?

If we start with n items:
After 1 comparison → n/2 items left
After 2 comparisons → n/4 items left
After 3 comparisons → n/8 items left … After k comparisons → 1 item left This means: n / (2^k) = 1 → 2^k = n → k = log₂(n) ✅ So in the worst case, binary search takes about log₂(n) steps to find the target (or determine it’s not there).

This makes it much faster than linear search (O(n)), especially on large datasets!

🐍 Binary Search in Python

# Define the binary search function
def binary_search(arr, target):
    # Set the left and right bounds of the list
    left, right = 0, len(arr) - 1

    # Continue the loop while the bounds have not crossed
    while left <= right:
        # Find the middle index
        mid = (left + right) // 2
        print(f"Checking index {mid}: {arr[mid]}")  # Debug print

        # If the middle value is the target, return the index
        if arr[mid] == target:
            return mid
        # If the target is greater, search the right half
        elif arr[mid] < target:
            left = mid + 1
        # If the target is smaller, search the left half
        else:
            right = mid - 1

    return -1  # If not found, return -1

# Example list
numbers = [1, 3, 5, 7, 9, 11, 13]

# Search for the number 7 in the list
print(binary_search(numbers, 7))  # Output: 3

Homework

PART A: Binary Breakdown

Decimal: 42

42 ÷ 2 = 21 remainder 0  
21 ÷ 2 = 10 remainder 1  
10 ÷ 2 = 5 remainder 0  
5 ÷ 2 = 2 remainder 1  
2 ÷ 2 = 1 remainder 0  
1 ÷ 2 = 0 remainder 1

**42** in binary = **101010**

Place Value Table:

| 2⁵ | 2⁴ | 2³ | 2² | 2¹ | 2⁰ |
|----|----|----|----|----|----|
| 1  | 0  | 1  | 0  | 1  | 0  |
| 32 | 0  | 8  | 0  | 2  | 0  |  
**Sum = 32 + 8 + 2 = 42**

Decimal: 19

19 ÷ 2 = 9 remainder 1  
9 ÷ 2 = 4 remainder 1  
4 ÷ 2 = 2 remainder 0  
2 ÷ 2 = 1 remainder 0  
1 ÷ 2 = 0 remainder 1

**19** in binary = **10011**

Place Value Table:

| 2⁴ | 2³ | 2² | 2¹ | 2⁰ |
|----|----|----|----|----|
| 1  | 0  | 0  | 1  | 1  |
| 16 | 0  | 0  | 2  | 1  |  
**Sum = 16 + 2 + 1 = 19**

Decimal: 100

100 ÷ 2 = 50 remainder 0  
50 ÷ 2 = 25 remainder 0  
25 ÷ 2 = 12 remainder 1  
12 ÷ 2 = 6 remainder 0  
6 ÷ 2 = 3 remainder 0  
3 ÷ 2 = 1 remainder 1  
1 ÷ 2 = 0 remainder 1

**100** in binary = **1100100**

Place Value Table:

| 2⁶ | 2⁵ | 2⁴ | 2³ | 2² | 2¹ | 2⁰ |
|----|----|----|----|----|----|----|
| 1  | 1  | 0  | 0  | 1  | 0  | 0  |
| 64 | 32 | 0  | 0  | 4  | 0  | 0  |  
**Sum = 64 + 32 + 4 = 100**

PART B: Binary to Decimal Sprint

Binary: 101010

| 2⁵ | 2⁴ | 2³ | 2² | 2¹ | 2⁰ |
|----|----|----|----|----|----|
| 1  | 0  | 1  | 0  | 1  | 0  |
| 32 | 0  | 8  | 0  | 2  | 0  |  
**Sum = 32 + 8 + 2 = 42**
As shown in the table above, I broke the binary number down and then found the value for each place and then added it all together. Same for the rest :D

Binary: 10011

| 2⁴ | 2³ | 2² | 2¹ | 2⁰ |
|----|----|----|----|----|
| 1  | 0  | 0  | 1  | 1  |
| 16 | 0  | 0  | 2  | 1  |  
**Sum = 16 + 2 + 1 = 19**

Binary: 110011

| 2⁵ | 2⁴ | 2³ | 2² | 2¹ | 2⁰ |
|----|----|----|----|----|----|
| 1  | 1  | 0  | 0  | 1  | 1  |
| 32 | 16 | 0  | 0  | 2  | 1  |  
**Sum = 32 + 16 + 2 + 1 = 51**

PART C: Binary Search in Action

List: [3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33]

**Search for 18**

Steps:
- 11 values, middle index = 5 → value = 1
- Found

**Comparisons made: 1**

**Search for 33**

Steps:
- Middle index = 5 → value = 18  
- 33 > 18 → Search right half  
- New middle = 8 → value = 27  
- 33 > 27 → Search right half  
- New middle = 10 → value = 33 
- Found

**Comparisons made: 3**

**Search for 5**

Steps:
- Middle index = 5 → value = 18  
- 5 < 18 → Search left half  
- New middle = 2 → value = 9  
- 5 < 9 → Search left half  
- New middle = 0 → value = 3  
- 5 > 3 → Search right → index 1 = 6  
- 5 < 6 → no more elements to check 
- Not found

**Comparisons made: 4**

PART D: Binary Search with Strings, Sorted!

List: ["apple", "banana", "carrot", "dragonfruit", "fig", "grape", "kiwi", "mango", "orange", "peach", "watermelon"]

Search for "mango"
- Middle = index 5 → "grape"  
- "mango" > "grape" → Search right  
- Middle = 8 → "orange"  
- "mango" < "orange" → Search left  
- Middle = 6 → "kiwi"  
- "mango" > "kiwi" → index 7 = "mango"
- Found

**Comparisons: 4**

Search for "carrot"
- Middle = 5 → "grape"  
- "carrot" < "grape" → Search left  
- Middle = 2 → "carrot" 
- Found

**Comparisons: 2**

Search for "lemon"
- Middle = 5 → "grape"  
- "lemon" > "grape" → Right  
- Middle = 8 → "orange"  
- "lemon" < "orange" → Left  
- Middle = 6 → "kiwi"  
- "lemon" > "kiwi" → index 7 = "mango"  
- "lemon" < "mango" → No more elements 
- Not found

**Comparisons: 4**

Free Response

Why is binary search more efficient for large data than linear search?

Binary search eliminates half the search space with each comparison, making it O(log n) instead of O(n) like linear search. This is much faster for large datasets.

What happens if the list isn’t sorted and you try to use binary search?

If the list isn’t sorted, binary search won’t work correctly—it might miss the target or give the wrong result entirely since it relies on the order to eliminate half the list.

Could you use binary search in a video game leaderboard or streaming service search bar? Why or why not?

Yes, if the data is sorted (e.g. leaderboard by score or search suggestions alphabetically), binary search can speed up lookups. But in real-time or fuzzy searches, other algorithms might be more appropriate.

List and Filtering

link

List: College Board Definition: A list is an ordered sequence of elements. The use of lists allows multiple related items to be represented using a single variable.

Benefits:

Real World examples: wishlists, inbox, spotify playlists, shopping carts

Working w lists

[,,,]
any datatype

Procedure*	Description	Example
`append(item)`	Adds an item to the end of the list	`scores.append(100)`
`insert(index, item)`	Inserts an item at a specific position	`scores.insert(1, 95)`
`remove(item)`	Removes the first matching item	`scores.remove(87)`
`pop(index)`	Removes and returns the item at the given index	`scores.pop(2)`
`len(list)`	Returns the number of items in the list	`len(scores)`
`slice[start:end]`	Returns a portion of the list	`scores[0:3]`
`sort()`	Sorts the list in ascending order	`scores.sort()`
`reverse()`	Reverses the order of the list	`scores.reverse()`
`clear()`	Removes all elements from the list	`scores.clear()`
`index(item)`	Returns the index of the first matching item	`scores.index(90)`

Traversing a list:

Traversing a list means going through each item one by one using a loop. Traversing lists are a key factor in creating filtering algorithms.
```
  colors = ["red", "blue", "green", "yellow"]

  for color in colors:
      print("Color:", color)
```

Filter Algorithms:

College Board states that an algorithim is “a finite set of instructions that accomplish a specific task.” They also say that “Filtering algorithims are important tools for finding information and recognizing patterns in data.”

Filtering algorithm: Loops through the list (TRAVERSAL LIST!), Checks a condition, Stores matching items in a new list.

 numbers = [3, 8, 12, 5, 7, 14]
 even_numbers = []

 for num in numbers:
     if num % 2 == 0:
         even_numbers.append(num)

 print(even_numbers)

 [8, 12, 14]

Relation to Flask Proj.:

Can filter through a database.
A user types in a specific filter (what they are looking for)
Flask filters matching items from a backend database (e.g. SQL)
Flask uses jsonify to return the filtered list to the frontend

Popcorn Hacks

Some benefits of using lists is to organize, filter, and store data. Some real world examples include online shopping carts, inboxes, anything that needs queueing or a line.
list: ["pen", "marker", "eraser", "sharpener"] returns: eraser
Real world examples of filtering algorithms include inboxes (unread/read), online cateloges, library (avaiable/unavailable), etc.

Homework

1.
fruit = ["apple", "mango", "banana", "orange", "kiwi"]
fruit.append("grape")  # List procedure: append
# This adds "grape" to the end of the list fruit
fruit.remove("banana")  # List procedure: remove
# This removes "banana" from the list fruit
fruit.sort()  # List procedure: sort
# This sorts the list fruit in alphabetical order
print(fruit)

['apple', 'grape', 'kiwi', 'mango', 'orange']

2. 
for i in fruit:
    print(i)
# This code traverses the list ruit and prints each item
# Instructions:
# 1. Start with the list `fruit`
# 2. Use a for-loop to visit each item one by one
# 3. The loop variable `i` holds the current fruit
# 4. You can apply any condition or action inside the loop (e.g., print, filter, etc.)

apple
grape
kiwi
mango
orange

3. 
import pandas as pd

# Step 1: Create a dataset (list of fruits and their weights)
fruit = {
    'type': ["apple", "mango", "banana", "orange", "kiwi"],
    'weight': [400, 600, 350, 780, 330]  # weights in grams
}

# Step 2: Convert the dictionary to a DataFrame
fruit_df = pd.DataFrame(fruit)

# Step 3: Define the filtering condition
# We want only the fruits that weigh less than 500 grams

# Step 4: Apply the filtering using boolean indexing
light_fruits = fruit_df[fruit_df['weight'] < 500]

# Step 5: Output the filtered list
print("Fruits weighing less than 500 grams:")
print(light_fruits)

Fruits weighing less than 500 grams:
     type  weight
0   apple     400
2  banana     350
4    kiwi     330

Simulation

If the seed the random generator is set to is the same, then it isn’t truly random because they are all human written and are following the same algorithm. If you were to set the seed to something such as OS time, then it’ll be more random.

Most random.randits will be followed by a conditional as the result will affect the conditional.

Simluation - program that models the behavior of a real-world process over time

allows for the exploration of systems
untangible (not physical)
used in game dev, physics engines, score progression, etc

Stimulation != Randomness

predictable things, stuch as a bouncing ball under gravity, where gravity is the same on Earth

Popcorn Hack 1:

A few real world applications for random number generations include video games and gambling. In video games, random numbers are used to generate unpredictable outcomes like loot drops, enemy behavior, or terrain generation. This adds variety and replayability, making games more engaging and dynamic. In gambling, random number generation ensures fairness and unpredictability in games like slots, roulette, or lottery draws. It prevents patterns or bias, which is crucial for maintaining trust and legal compliance.

import random

# Generate random integer between a and b inclusive
def random_int(a, b):
    return random.randint(a, b)

# Examples
print(f"Random number between 1-10: {random_int(1, 10)}")
print(f"Random number between 0-1: {random_int(0, 1)}")  # Coin flip
print(f"Random number between 1-6: {random_int(1, 6)}")  # Die roll

Random number between 1-10: 10
Random number between 0-1: 0
Random number between 1-6: 5

Popcorn Hack 2:

import random

def magic_8_ball():
    num = random.randint(1,4)

    if num <= 2: 
        return "Yes"
    elif num == 3:
        return "No"
    else:
        return "Ask again later"

# Test your function
for i in range(10):
    print(f"Magic 8-Ball says: {magic_8_ball()}")

Magic 8-Ball says: Yes
Magic 8-Ball says: Yes
Magic 8-Ball says: No
Magic 8-Ball says: No
Magic 8-Ball says: Yes
Magic 8-Ball says: Yes
Magic 8-Ball says: Yes
Magic 8-Ball says: Ask again later
Magic 8-Ball says: Ask again later
Magic 8-Ball says: No

Popcorn Hack 3:

This is a simulation because it models the behavior of a real-world system, in this case a traffic light, over time using code. Its real-world impact lies in how simulations like this help engineers design and test traffic systems for safety and efficiency before implementing them in actual intersections.

# Traffic light simulation (no randomness)

states = ["Green", "Yellow", "Red"]
durations = {"Green": 5, "Yellow": 2, "Red": 4}
timeline = []

# Simulate 10 time steps
time = 0
state = "Green"
counter = 0

while time <20:
    timeline.append((time, state))
    counter += 1
    if counter == durations[state]:
        counter = 0
        current_index = states.index(state)
        state = states[(current_index + 1) % len(states)]
    time += 1

for t, s in timeline:
    print(f"Time {t}: {s}")

Time 0: Green
Time 1: Green
Time 2: Green
Time 3: Green
Time 4: Green
Time 5: Yellow
Time 6: Yellow
Time 7: Red
Time 8: Red
Time 9: Red
Time 10: Red
Time 11: Green
Time 12: Green
Time 13: Green
Time 14: Green
Time 15: Green
Time 16: Yellow
Time 17: Yellow
Time 18: Red
Time 19: Red

Homework

Create a dice game with the following features:

Player rolls two dice
If the sum is 7 or 11, player wins
If the sum is 2, 3, or 12, player loses
If the sum is any other number, that becomes the “point”
Player continues to roll until they either roll the point again (win) or roll a 7 (lose)
Track win/loss statistics

import random

def roll_dice():
    """Roll two dice and return their values and sum."""
    die1 = random.randint(1, 6)
    die2 = random.randint(1, 6)
    total = die1 + die2
    print(f"You rolled: {die1} + {die2} = {total}")
    return die1, die2, total

def play_dice_game():
    """
    Play one round of the dice game.
    Returns True if player wins, False if player loses.
    """
    _, _, total = roll_dice()
    
    if total in (7, 11):
        print("You win!")
        return True
    elif total in (2, 3, 12):
        print("You lose!")
        return False
    else:
        point = total
        print(f"Your point is now {point}. Keep rolling!")
        
        while True:
            _, _, total = roll_dice()
            if total == point:
                print("You hit your point again! You win!")
                return True
            elif total == 7:
                print("You rolled a 7. You lose!")
                return False

def main():
    """Main game function with game loop and statistics."""
    wins = 0
    losses = 0

    while True:
        play = input("\nDo you want to play a round? (y/n): ").strip().lower()
        if play == 'y':
            result = play_dice_game()
            if result:
                wins += 1
            else:
                losses += 1
            print(f"Current Stats -> Wins: {wins}, Losses: {losses}")
        elif play == 'n':
            print("\nFinal Statistics:")
            print(f"Wins: {wins}, Losses: {losses}")
            break
        else:
            print("Invalid input. Please enter 'y' or 'n'.")

if __name__ == "__main__":
    print("Welcome to the Dice Game!")
    main()

Welcome to the Dice Game!
You rolled: 5 + 6 = 11
You win!
Current Stats -> Wins: 1, Losses: 0
You rolled: 6 + 4 = 10
Your point is now 10. Keep rolling!
You rolled: 1 + 6 = 7
You rolled a 7. You lose!
Current Stats -> Wins: 1, Losses: 1
You rolled: 4 + 6 = 10
Your point is now 10. Keep rolling!
You rolled: 5 + 3 = 8
You rolled: 1 + 2 = 3
You rolled: 5 + 2 = 7
You rolled a 7. You lose!
Current Stats -> Wins: 1, Losses: 2

Final Statistics:
Wins: 1, Losses: 2

Big O and Algorithmic Efficiency

link

Efficiency is impt - minimizes waiting time
decreases memory and cpu
scalabilty - can perform well with large scale stuff

Aspect comparison

performace - faster execution and reponsiveness
resource utilization

Algorithmic Efficiency

Time Eff. - how many operations are performed relative to the input size
Space Eff. - how much extra memory is required Energy Eff. - particularly import for mobile devices - less processing = longer batter life

Big O

focuses on worst case scenario

Popcorn Hack 1

Methods with constant complexity is most efficient 2 amd 3 are the most efficient. Both 2 and 3 are O(1) is time completixy as they work instantly, regardless of the number’s size. Modulus is direct to let you know whether a number is even or odd, while checking the last digit of a number doesn’t need additional compution.

Popcorn Hack 2

What is the time complexity of each algorithm? O(Logn) How many times faster is binary search than linear search? ~12345x What happens if you increase data_size to 20000000? Binary is now only ~1754x faster than linear search, and it took much longer for the program to run (24.3s vs 7.1s).

import time
import random

# Generate a large sorted list
data_size = 10000000
sorted_data = sorted(random.sample(range(100000000), data_size))

# Target to find (worst case for linear search)
target = sorted_data[-1]  # Last element

# O(n) - Linear Search
def linear_search(arr, target):
    for i, element in enumerate(arr):
        if element == target:
            return i
    return -1

# O(log n) - Binary Search
def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    
    return -1

# Compare performance
print("Testing with data size:", data_size)

start = time.time()
linear_result = linear_search(sorted_data, target)
linear_time = time.time() - start
print(f"Linear search: {linear_time:.6f} seconds")

start = time.time()
binary_result = binary_search(sorted_data, target)
binary_time = time.time() - start
print(f"Binary search: {binary_time:.6f} seconds")

print(f"Binary search is approximately {linear_time/binary_time:.0f}x faster")

Testing with data size: 10000000
Linear search: 4.851169 seconds
Binary search: 0.000047 seconds
Binary search is approximately 103286x faster

Homework Pt1: Sorting Showdown

import random
import time

# Bubble Sort function
def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

# Merge Sort function
def merge_sort(arr):
    if len(arr) > 1:
        mid = len(arr) // 2
        left = arr[:mid]
        right = arr[mid:]
        merge_sort(left)
        merge_sort(right)

        i = j = k = 0
        # Merge the sorted halves
        while i < len(left) and j < len(right):
            if left[i] < right[j]:
                arr[k] = left[i]
                i += 1
            else:
                arr[k] = right[j]
                j += 1
            k += 1
        while i < len(left):
            arr[k] = left[i]
            i += 1
            k += 1
        while j < len(right):
            arr[k] = right[j]
            j += 1
            k += 1

original_list = [random.randint(1, 1000) for _ in range(100)]

list_for_bubble = original_list[:]
list_for_merge = original_list[:]

start_bubble = time.time()
bubble_sort(list_for_bubble)
end_bubble = time.time()
bubble_time = end_bubble - start_bubble

start_merge = time.time()
merge_sort(list_for_merge)
end_merge = time.time()
merge_time = end_merge - start_merge

print(f"Bubble Sort time: {bubble_time:.6f} seconds")
print(f"Merge Sort time: {merge_time:.6f} seconds")
faster = "Merge Sort" if merge_time < bubble_time else "Bubble Sort"
print(f"Faster algorithm: {faster}")

# Merge Sort is faster because it has a time complexity of O(n log n), while Bubble Sort is O(n^2). Merge Sort divides the list and sorts recursively, which is far more efficient for larger datasets.

Bubble Sort time: 0.000190 seconds
Merge Sort time: 0.000093 seconds
Faster algorithm: Merge Sort

Homework Pt2: Search Race

import random

# Linear Search Function
def linear_search(arr, target):
    count = 0
    for i in range(len(arr)):
        count += 1
        if arr[i] == target:
            return count
    return -1

# Binary Search Function
def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    count = 0
    while left <= right:
        count += 1
        mid = (left + right) // 2
        if arr[mid] == target:
            return count
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

sorted_list = list(range(1, 100001))

target = random.choice(sorted_list)

linear_comparisons = linear_search(sorted_list, target)
binary_comparisons = binary_search(sorted_list, target)

print(f"Target number: {target}")
print(f"Linear Search comparisons: {linear_comparisons}")
print(f"Binary Search comparisons: {binary_comparisons}")

# Binary Search is significantly faster because it cuts the list in half with each comparison (O(log n)). Linear Search checks each element one by one (O(n)), making it much slower on large lists. If you run both searches on an unsorted list, Binary Search will not work correctly on an unsorted list—it depends on order to eliminate half the options. Linear Search still works fine because it simply checks every element regardless of order.

Target number: 22508
Linear Search comparisons: 22508
Binary Search comparisons: 17

Undecidable Problems

link

Undecidable problems - No yes or no output could be given

Graphs

Popcorn Hack

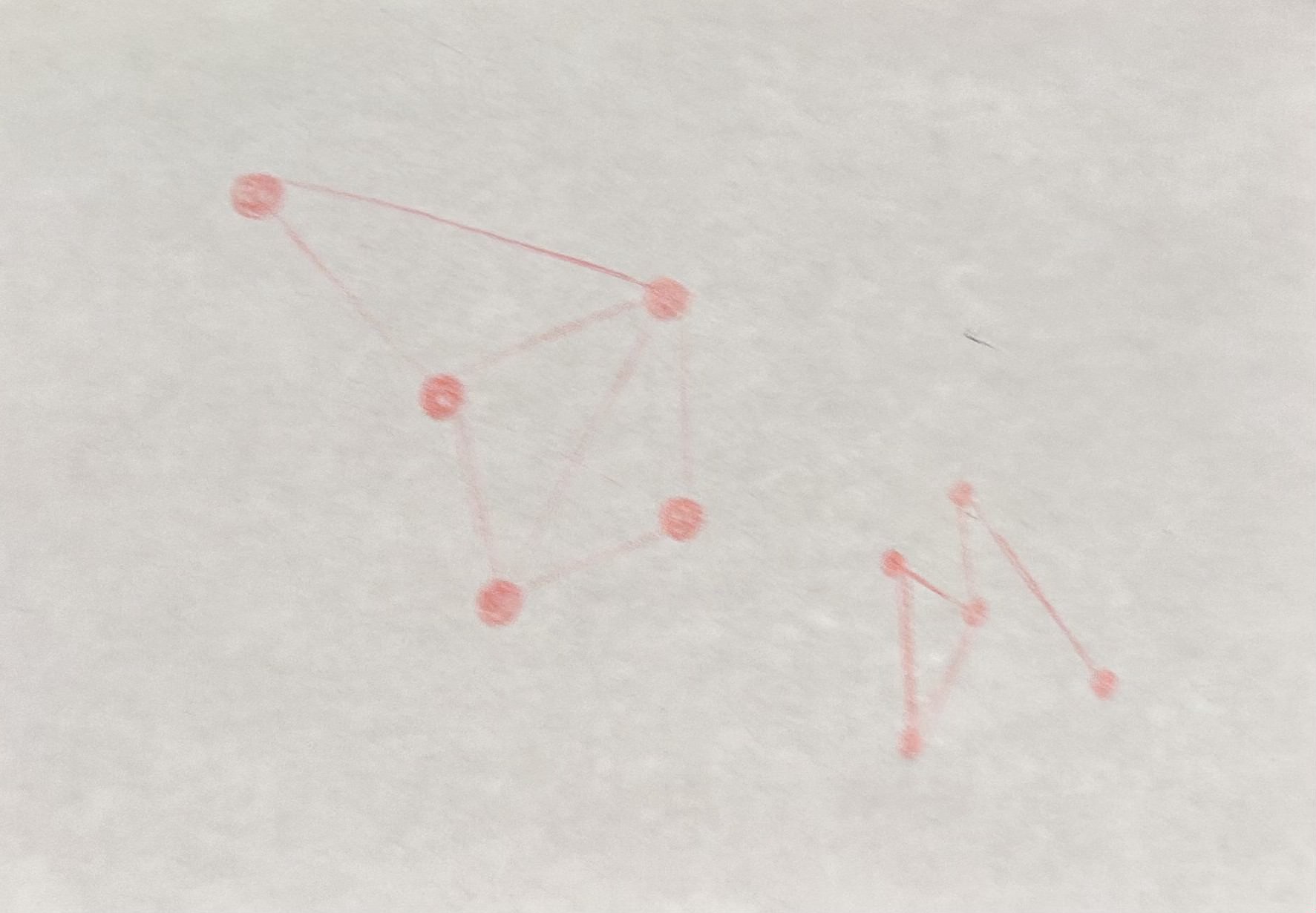
Homework

Q1: C

Q2: B - 2 connections

Heurisitics

Popcorn Hack

def greedy_coin_change(amount, coins=[25, 10, 5, 1]):
    change = []
    for coin in coins:
        while amount >= coin:
            amount -= coin
            change.append(coin)
    return change

# Example usage:
amount = 63
result = greedy_coin_change(amount)
print(f"Change for {amount}¢: {result}")
print(f"Total coins used: {len(result)}")

Change for 63¢: [25, 25, 10, 1, 1, 1]
Total coins used: 6

def greedy_coin_change(amount, coins=[1, 5, 10, 25]):
    change = []
    for coin in coins:
        while amount >= coin:
            amount -= coin
            change.append(coin)
    return change

# Example usage:
amount = 63
result = greedy_coin_change(amount)
print(f"Change for {amount}¢: {result}")
print(f"Total coins used: {len(result)}")

Change for 63¢: [1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Total coins used: 63

It is much less efficient as it only uses pennies. Thus, starting from a large value first is most more logical.

Homework

How did changing the order of coins affect the result? Changing the order of the coins meant that it only used the smallest value, which was a penny, and was thus very innefficient.

Which algorithm used fewer coins? The unchanged one where it started with the largest coin ammount first.

Where might greedy algorithms work well? Where might they fail? Greedy algorithms work well in situations where making a smaller optimal choice at each step leads to a altogether more optimal solution. This works well in things like coin demoninations. But they don’t work where local choices don’t lead to the best overall result.

What is one thing you changed, and what did it show you? One thing I changed was the order of the coin denominations from largest to smallest to smallest to largest. This change showed that the greedy algorithm’s success is highly dependent on the input order, and that without careful ordering, it may produce suboptimal results.

Undecidable Problems

Popcorn Hack 1

num = 10

while num != 0:
    print(num)
    num -= 1

while num != 0:
    print(num)
    num += 1

This is a undecidable problem because there is no real way of knowing in advance whether a loop like this will stop or not. It is trying to deterine whether to end the loop or not, but the computer can’t determine that before running the code.

Popcorn Hack 2

An algorithm can be used to solve an undecidable problem (True or False) False. If the problem is undecidable then that means there is no algorithm that can produce a correct yes or no answer for every possible input.
If a programmer encounters an undecidable problem, they can just use an algorithm that works most of the time. (True or False) False. For a undecidable problem, an algorithm that only works sometimes still doesn’t solve the problem completely. The programmer would need to redefine the problem or find a different approach.

Homework

1. 
Part 1: Identify the Problem Type Read the following problems and decide whether they are decidable or undecidable. Write your answer and a short reason why.

“Is this number divisible by 2?” Decidable because a algorithm can check if it is devisible or not and return a yes or no. 

“Will this program stop or run forever?” Undecidable. The typical scenario where it cnanot be solved by any algorithm. 

“Does this sentence contain the word ‘banana’?” Decidable. A computer can check for the word banana and return a yes or no.

“Will this AI ever become sentient?” Undecidable. There's no algorithm that can determine the future because of unpredictable/undefined factors. 

2. 
Algorithm Detective (2 minutes) Look at the two mystery “algorithms” below. Figure out which one is decidable and which one is undecidable, then explain your reasoning in one sentence each.

Step 1: Input a number  
Step 2: If the number is even, say "Yes." If not, say "No."  
Decidable because an algorithm is able to check for even or not. 

Step 1: Input any program  
Step 2: Predict if it will ever stop running  
Step 3: Output "Yes" if it will stop, "No" if it will run forever  
Undecidable because an algorithm cannot check whether something will end or not. 

3. 
Real-Life Connection: Think of something in real life where you can’t be sure what will happen unless you go through the entire experience. An example is sending a text to someone and waiting for a reply. You don't know if they're going to respond eventually, or it they'll never respond at all. 

Base 2 Math and Logic Gates

Binary is easiler to store, compress, etc. Used for pics e.g. jpg

Popcorn Hack 1

101010 = 2^1 + 2^3 + 2^5 = 42

12301 = not binary

11001 = 2^0 + 2^3 + 2^4 = 1 + 8 + 16 = 25

Popcorn Hack 2

101 + 110 = 1011

1101 - 1011 = 0010

111 + 1001 = 1110

Popcorn Hack 1

True or False and False -> True or False -> True

Popcorn Hack 2

not True and False -> False and False -> False

Popcorn Hack 3

True or False and not False -> True or False and True -> True or False -> True

Homework

#binary calculator
# Function to convert decimal to binary
def decimal_to_binary(decimal_num):
    if decimal_num >= 0:
        return bin(decimal_num)[2:]  # Remove the '0b' prefix
    else:
        return '-' + bin(abs(decimal_num))[2:]

# Function to convert binary to decimal
def binary_to_decimal(binary_str):
    if binary_str.startswith('-'):
        return -int(binary_str[1:], 2)
    else:
        return int(binary_str, 2)

# Test cases
print("Decimal to Binary:")
print("10 →", decimal_to_binary(10))       # 1010
print("-10 →", decimal_to_binary(-10))     # -1010

print("\nBinary to Decimal:")
print("1010 →", binary_to_decimal("1010"))     # 10
print("-1010 →", binary_to_decimal("-1010"))   # -10

#difficulty level checker
import time

difficulty = input("Enter difficulty (easy, medium, hard): ").lower().strip()

while difficulty not in ["easy", "medium", "hard"]:
    print("Please enter a valid difficulty level.")
    difficulty = input("Enter difficulty (easy, medium, hard): ").lower().strip()
    time.sleep(0.5)

print("Difficulty set to:", difficulty)

Base 64

PH 1

Which image format is best for logos and transparency? PNG - supports transparency and preserves image quality.

Which format loses quality to make the file size smaller? JPG / JPEG - uses lossy compression to shrink file size.

Which format is used for simple animations, like memes? GIF - supports basic animations and limited color.

PH 2

What does this Base64 string decode to? U1Q= U1Q= → ST

U = 20 → 010100
1 = 53 → 110101
Q = 16 → 010000

Together = 01010011

01010100 = ASCII for “ST”

Hmwk 1, 2

http://kchen8478.github.io/katherine_2025/website/